
The image below shows all cases where the right angle may appear.
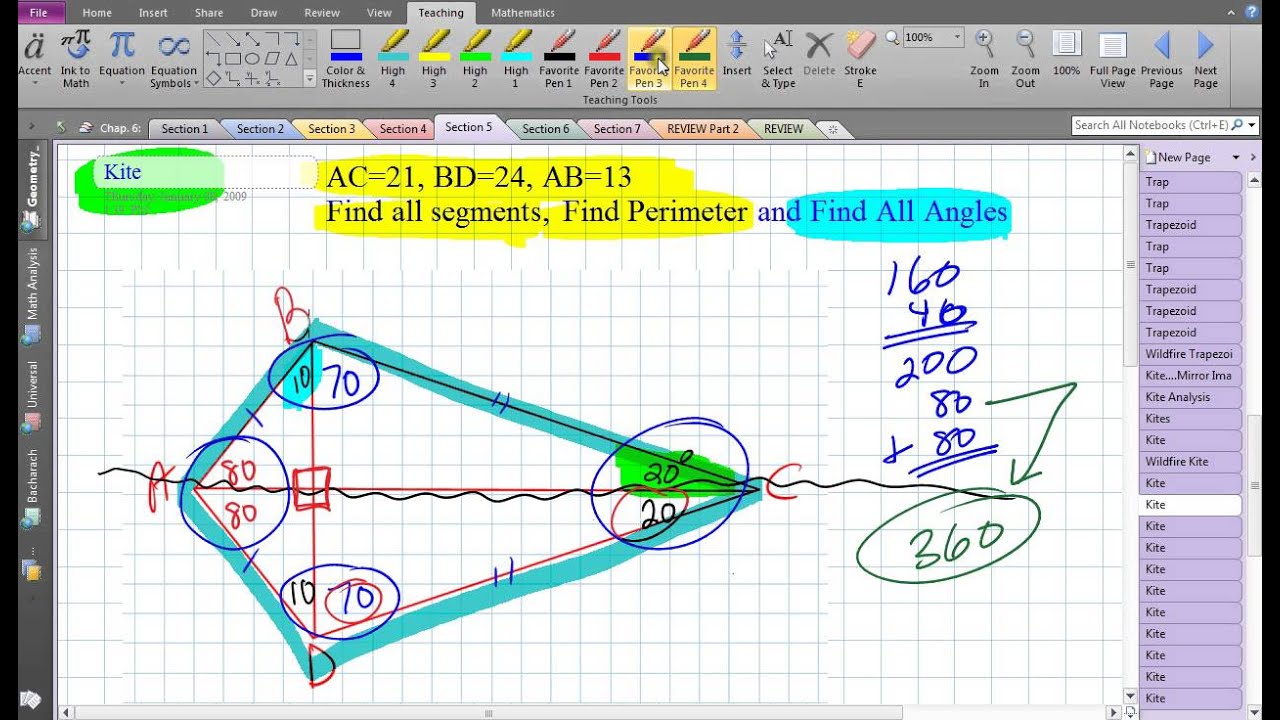
There is one special type of kite called the " right kite " which contains one or two right angles. Inscribe the circle using point E as its center and line EF as its radius. from point E, draw a perpendicular to any of the four sides. bisect one of the non-vertex angles (B or C) and extend this line so that it meets line AD at point E To inscribe a circle graphically (using compass and straight edge) within a kite: (Basically, this means that the circle is tangent to each of the four sides of the kite.) Read the next paragraph for more information.Īll kites are tangential quadrilaterals, meaning that they are 4 sided figures into which a circle (called an incircle) can be inscribed such that each of the four sides will touch the circle at only one point. The last two output boxes (" Line AE" and " radius") are for inscribing a circle within a kite. If you know 3 data items of a kite, click on one of the eight buttons above that correspond to the 3 data items you know.Įnter those numbers and then click "CALCULATE" to see the answers. a diagonal (line BC) that divides the kite into two isoceles triangles (ABC and BCD) a diagonal, called the axis of symmetry (line AD), that bisects the other diagonal (line BC), bisects the vertex angles (A and D) and divides the kite into two congruent triangles (ABD and ACD) diagonals which always meet at right angles two equal angles (B and C) called non-vertex angles two pairs of equal, adjacent sides (a and b) no concave (greater than 180°) internal angles
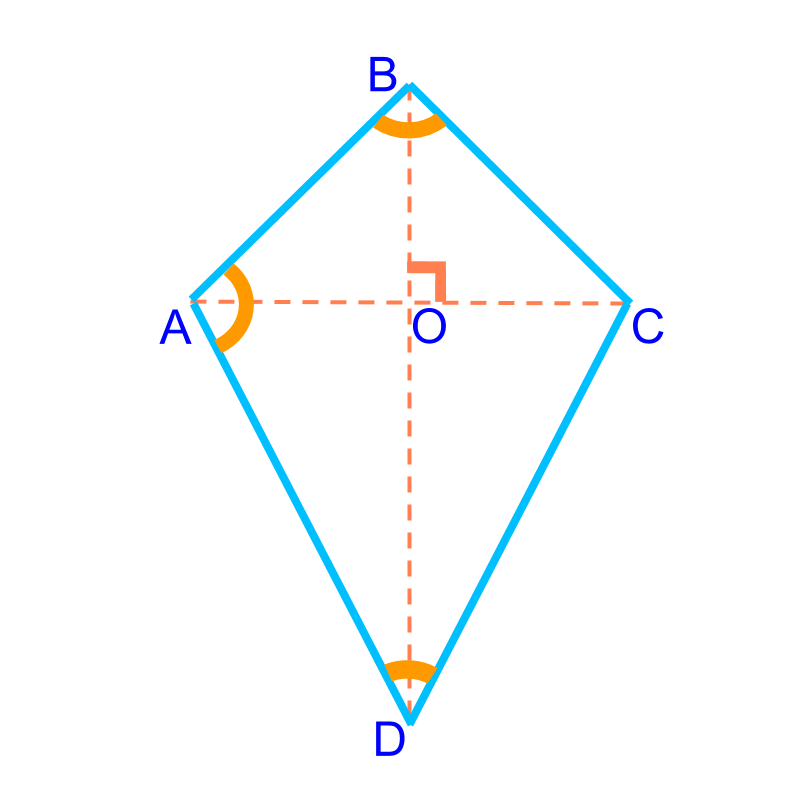
For a square and rectangle calculator, click here squares.Īll kites are quadrilaterals with the following properties: For a rhombus calculator, click here rhombuses. For a parallelogram calculator, click here parallelograms.
For a trapezoid calculator, click here trapezoids. Scroll Down for instructions and definitions Click here to see information for all quadrilaterals.


 0 kommentar(er)
0 kommentar(er)
